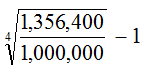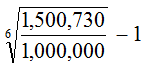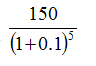สวัสดีครับ หลังจากเราเข้าใจแล้วว่าดอกเบี้ยทบต้นคืออะไร ทีนี้ต่อไปที่ต้องรู้คือแล้วเราจะคำนวนหามันอย่างไร บางคนถามเคยถามผมว่าต้องคำนวนด้วยเหรอ ไม่ต้องรู้ได้มั้ยไม่ชอบสูตรไม่ชอบเลข กดเครื่องคิดเลขเอาได้มั้ย ผมจะบอกว่าคุณใจเย็นๆมันไม่ยากเกินคุณแน่นอน ถ้าคุณคำนวนไม่ได้หรือไม่เข้าใจเรื่องนี้นะ เสียเปรียบโคตร ผมยกตัวอย่างนะครับ
สมมติมีคนสองคนมาขอยืมเงินคุณน่ะ ทั้งสองคนอยากยืมคนละ 1,000,000 บาท แต่คุณมีเงินล้านเดียว คุณจะให้ใคร
คนแรกบอก ถ้าให้เค้ายืมนะ อีก 4 ปี เค้าจะคืนคุณเป็นเงิน 1,356,400 บาท
คนที่สองบอก ถ้าให้เค้ายืมนะ อีก 6 ปี เค้าจะคืนคุณเป็นเงิน 1,500,730 บาท
มึนมั้ยครับ ถ้าไม่มีวิธีเปรียบเทียบมันจะความรู้สึกแบบนี้แหละครับ คุณอาจเผลอไปเลือกคนที่ให้ผลตอบแทนน้อยกว่าก็ได้ สุดท้ายการลงทุนถ้ามันต้องมีหน่วยกลางครับ ซึ่งปกติแล้วคนเค้าจะใช้อัตราดอกเบี้ยทบต้นต่อปีเป็นตัวหลักครับ ต่อไปนี้ผมจะสอนคุณทำเรื่องนี้ วันหลังจะไม่มีใครมาทำคุณงงได้อีก ผมรู้เพราะสมัยเรียนเคยงงมาก่อนครับ
ว่าแล้วตั้งใจอ่านดีๆครับ อย่าตกใจกับเลข ค่อยๆอ่าน ต่อจากนี้เราจะใช้ตัวแปรตามความหมายนี้
PV = Present value
หรือมูลค่าปัจจุบัน ว่าง่ายๆคือเงินตอนเริ่มต้นนะ
FV = Future value
หรือมูลค่าในอนาคต ซึ่งคือเงินตอนท้ายที่เราจะพิจารณา
n = Number of period
หรือจำนวนหน่วยเวลา (ปี, เดือน, วัน, รายสามเดือน หรืออะไรก็แล้วแต่)
r = Compound rate
หรืออัตราดอกเบี้ยทบต้น (หน่วยจะเป็น เปอร์เซนต์ต่อหนึ่งหน่วยเวลา)
สมมติ เราไปฝากเงิน 100 บาท (PV) ดอกเบี้ยธนาคารอยู่ที่ 3% (r) หนึ่งปีผ่านไปเราจะได้ดอกเบี้ย 3 บาทครับ คือมาจากเอา 3% ไปคูณกับเงินต้น 100 บาทได้เป็นดอกเบี้ย เมื่อเอาดอกเบี้ยที่ได้ไปรวมกับเงินต้นรวมเงินในบัญชีเป็น 103 บาท
ตอนนี้ ปีที่ 1
เงินต้นจากปีก่อน + ดอกเบี้ยที่ได้ในปีนั้น
100 –> 100 + (3% × 100)
–> 100 + (0.03 × 100)
–> 100 (1 + 0.03)
จากข้างบนจะเห็นว่า เมื่อผ่านไปหนึ่งปี เงินจะโตเท่าไหร่หาได้จากการเอา เงินต้น x (1 + อัตราดอกเบี้ยทบต้น)
แล้วถ้าผ่านไปอีก 1 ปีล่ะ
ปีที่ 1 ปีที่ 2
เงินต้นจ่ากปีก่อน + ดอกเบี้ยที่ได้ในปีนั้น
[100 (1 + 0.03)] –> [100 (1 + 0.03)] + (3% × [100 (1 + 0.03)])
–> [100 (1 + 0.03)] + (0.03 × [100 (1 + 0.03)])
–> [100 (1 + 0.03)] (1 + 0.03)
–> 100 (1 + 0.03)2
คุณจะเห็นได้ว่า ถ้าคุณจะหาเงินในอนาคตเมื่อผ่านไป 1 ปี จะได้เท่ากับ 100 (1 + 0.03)
คุณจะเห็นได้ว่า ถ้าคุณจะหาเงินในอนาคตเมื่อผ่านไป 2 ปี จะได้เท่ากับ 100 (1 + 0.03)2
คุณจะเห็นได้ว่า ถ้าคุณจะหาเงินในอนาคตเมื่อผ่านไป 3 ปี จะได้เท่ากับ 100 (1 + 0.03)3
จึงเป็นที่มาสูตรว่า
เงินอนาคต = เงินต้น (1 + อัตราดอกเบี้ยทบต้น)จำนวนหน่วยเวลา
FV = PV (1 + r)n
แล้วเราก็ลองมาใช้กับปัญหาตอนแรกที่ผมให้เลือกว่าจะให้ใครยืมเงิน คุณจะตัดสินใจเลือกโดยหาว่า r ของการให้สองคนนี้ยืมเงิน คนไหนให้ r มากกว่ากัน
คนแรกบอก ถ้าให้เค้ายืม 1,000,000 บาทนะ อีก 4 ปี เค้าจะคืนคุณเป็นเงิน 1,356,400 บาท
1,356,400 = 1,000,000 (1 + r)4
ใช้ excel หรืออะไรหาค่าเอาครับ จะได้ r = 7.92% ต่อปี
คนที่สองบอก ถ้าให้เค้ายืม 1,000,000 บาทนะ อีก 6 ปี เค้าจะคืนคุณเป็นเงิน 1,500,730 บาท
1,500,730 = 1,000,000 (1 + r)6
ใช้ excel หรืออะไรหาค่าเอาครับ จะได้ r = 7% ต่อปี
จะเห็นว่าลงทุนกับคนแรกจริงๆได้เยอะกว่าครับ
และคุณก็สามารถเอาสูตรนี้ไปหาอย่างอื่นได้เช่น เอาไปหาราคาเป้าหมายที่คุณจะซื้อหุ้นครับ สมมติถ้าคุณรู้ว่าอนาคตหุ้นตัวนี้อีก 5 ปีน่าจะมีราคาประมาณ 150 บาท คุณวางแผนอยากได้ผลตอบแทนต่อปีซัก 10% คุณก็แค่แทนค่าหา PV ว่าคุณต้องซื้อที่ราคาอะไรถึงจะได้ 10% ต่อปีเป็นระยะเวลา 5 ปี
FV = PV (1 + r)n
150 = PV (1 + 0.1)5
แก้สมการหา PV กรณีนี้ได้ 93.12 บาท
แปลว่า ถ้าคุณคิดว่าหุ้นนี้จะราคา 150 บาทใน 5 ปีข้างหน้า แล้วคุณอยากได้ 10% ต่อปี แปลว่าคุณต้องซื้อตอนนี้ที่ 93.12 บาทครับ
มาถึงตอนนี้คุณก็จะทราบที่มาของสูตรคำนวนหา PV, FV, n หรือ r ละครับ แน่นอนว่าคุณสามารถใช้เครื่องคิดเลขไฟแนนซ์ก็จะทำได้ง่ายไม่ต้องตั้งสมการอะไร แต่ผมอยากให้คุณเข้าใจเอาไว้ เพราะอนาคตถ้าคุณไปคำนวนหาผลตอบแทนพวกกรมธรรม์ประกันชีวิต หรืออะไรพวกนี้ มันต้องใช้ความเข้าใจพื้นฐานที่ดีครับไม่งั้นทำไม่ได้ ขอบคุณที่ตั้งใจอ่านครับ